Binary search is a highly efficient algorithm for finding elements in arrays, reducing the search range by half with each iteration. Think of it like searching for a word in a physical dictionary.
Binary search is also referred to as half-interval search, which gives us a hint at when to use it. If we can, roughly, eliminate half of the search area with a single condition, then we are binary searching our target.
Here’s a simplified explanation:
Given a sorted array of integers and a target integer, the goal is to find the index of the target element. If it’s not found, return -1.
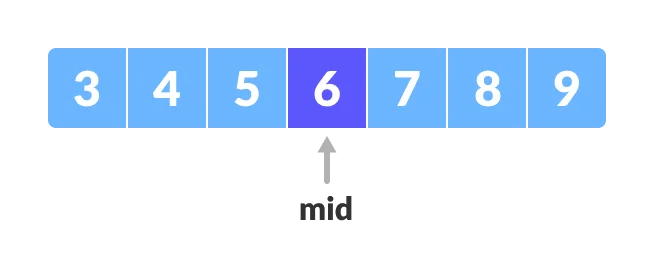
The key insight is leveraging the sorted nature of the array. Initially, a random element is selected and compared to the target:
If it’s a match, we’re done; return its index.
If the element is smaller, eliminate the left section of the array; if larger, eliminate the right section.
Repeat this process until the target is found. Always pick the middle element to halve the search space, achieving a runtime of O(log(N)) Time Complexity.
Binary search can be implemented
- Iteratively O(1) memory | space complexity
- Recursively O(log(N)) memory [ for storing function calls in stack memory].
The structure of a successful Binary Search typically consists of three primary components:
Pre-processing: Organizing the collection by sorting it if it’s unsorted.
Binary Search: Employing either a loop or recursion to halve the search space with each comparison.
Post-processing: Identifying feasible candidates within the remaining space.
One of the primary reasons for candidates stumbling in binary search coding interviews is their oversight of edge cases.
Various scenarios can lead to edge cases in binary search. For example, an edge case occurs when the target resides at the 0th index of an array, when it’s at the (n — 1)th index, or when the loop becomes infinite.
Fortunately, these potential pitfalls can be sidestepped by consistently employing the same approach.
Template:
def binarySearch(arr, target):
L, R = 0, len(arr) - 1
while L <= R:
mid = (L + R) // 2
if target > arr[mid]:
L = mid + 1
elif target < arr[mid]:
R = mid - 1
else:
return mid
return -1Sample Program:
def binarySearch(nums, target):
if len(nums) == 0:
return -1
# the initial value for left index is 0
left = 0
# the initial value for right index is the number of elements in the array
right = len(nums)
# left + 1 >= right will finish while loop
while left + 1 < right:
mid = (right + left) // 2;
if nums[mid] == target:
# mid is the index of the target
return mid
elif nums[mid] < target:
# there is no sense to search in the left half of the array
left = mid
else:
# there is no sense to search in the right half of the array
right = mid
# left can be the index of the target
if nums[left] == target:
return left
# the target doesn't exist in the array
return -1
def main():
nums = [1,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59];
print("Index of 37 is ---> " + str(binarySearch(nums, 37)))
print("Index of 1 is ---> " + str(binarySearch(nums, 1)))
print("Index of 59 is ---> " + str(binarySearch(nums, 59)))
print("Index of 25 is ---> " + str(binarySearch(nums, 25)))
main()
Fascinatingly, binary search extends its functionality beyond sorted arrays. It can be applied whenever you need to make binary decisions to narrow down the search range.
Leet code Problems to practice:
Please find all the Tagged Leet code questions here: https://leetcode.com/tag/binary-search/
And also check this post in Leet code, Because this person explained the Binary search template with some examples and how to apply the same template for medium and hard problems. Specifically for the problems involving solution space.
https://leetcode.com/discuss/study-guide/786126/python-powerful-ultimate-binary-search-template-solved-many-problems/2387053
Happy Coding :-)